گرافن، جادوی قرن بیست و یکم
گرافن را «ماده جادویی» قرن 21 مینامند. این ماده که گفته میشود محکمترین مادهای است که تاکنون مورد مطالعه قرار گرفته، جایگزینی برای سیلیکون است و خواص عجیب آن مانند بیشترین میزان رسانایی الکتریکی در بین مواد شناخته شده، دنیای علم و رسانهها) را تکان داده است .گرافن ماده ای منحصربه فرد با پایهی کربنی و دانسیتهی اتمی بالاست. ترکیب غیر عادی خواص آن نظیر سختی و استحکام مکانیکی بسیار بالا، رسانایی الکتریکی و حرارتی بالا و قابل تنظیم، خصوصیات عالی نوری وسطحی است وازطریق عامل دار کردن شیمیایی ،موردتوجه خاص محققان قرارگرفته است و این حقیقت که شیمیدانان به سختی میتوانند جایگزینی برای گرافن پیدا کنند، سبب شده که این ماده دارای کاربردهای فراوانی در نانوالکترونیک، پیلهای خورشیدی و ابزارهای ذخیره انرژی مثل باطری ها و ابرخازنها باشد.
معرفی گرافن( Graphene)
اما گرافنچیست؟
جدیدترین تعریفی که برای گرافن ارائه شده این است که: گرافن مادهای تخت و تکلایه متشکل از اتمهای کربن است که این اتمها در یک شبکه دوبعدی و کندو مانند به هم متصل شدهاند و این ساختاری است که همه مواد گرافنی در ابعاد دیگر نیز از آن تبعیت میکنند.این ماده دارای ضخامت یک اتم با ویژگیهای منحصربهفرد است ،که به دلیل ضخامت کم این ماده را به عنوان باریک ترین ماده جهان نیز می شناسند. درواقع گرافن اصطلاحی هست که به نوارهای بسیار نازکی از تک لایه های گرافیت گفته می شود،اگر گرافیت را یک دفترچه از صفحات موازی در نظر بگیریم ،به هر ورق آن گرافن گفته می شود.
همان طور که می دانیم گرافیت یکی از آلوتروپ های (اشکال)کربن است. یکی از راه های تولید گرافن این است که اینقدر لایه های گرافیت را از هم دور کنیم تا به گرافن تبدیل شود. (ورقه ورقه کردن گرافیت )
همان طور که گفتیم صفحات گرافن با کنار هم قرار گرفتن اتمهای کربن تشکیل میشوند. در یک صفحه گرافن، هر اتم کربن با 3 اتم کربن دیگر پیوند داده است. این سه پیوند در یک صفحه قرار دارند و زوایای بین آنها با یکدیگر مساوی و برابر با 120 درجه است. در این حالت، اتمهای کربن در وضعیتی قرار میگیرند که شبکهای از شش ضلعیهای منتظم را ایجاد میکنند. البته این ایدهآلترین حالت یک صفحهی گرافن است. در برخی مواقع، شکل این صفحه به گونهای تغییر میکند که در آن پنجضلعیها و هفتضلعیهایی نیز ایجاد میشود.

ساختار اتمی صفحه گرافن: در این تصویر اتمهای کربن با نقاط سیاه و پیوندها با نقطه چین نمایش داده شدهاند.
در یک صفحه گرافن، هر اتم کربن یک پیوند آزاد در خارج از صفحه دارد. این پیوند مکان مناسبی برای قرارگیری برخی گروههای عاملی و هم چنین اتمهای هیدروژن است. پیوند بین اتمهای کربن در اینجا کوالانسی بوده و بسیار محکم است. بنابراین گرافن استحکام بسیار زیادی دارد .گفتیم گرافیت نیز که یک مادهی کربنی پر مصرف و شناخته شده است، از روی هم قرار لایههای گرافن و تشکیل یک ساختار منظم تشکیل میشود. اما همانطور که میدانیم، گرافیت بسیار نرم است.
به نظر شما دلیل این امر چیست؟
آنچه لایه های گرافن را روی یکدیگر نگه میدارد، پیوندهای واندروالس بین آنهاست. این پیوند بسیار ضعیف است. بنابراین لایههای گرافن به راحتی میتوانند روی هم بلغزند و به همین دلیل گرافیت (نوک مداد سیاه) نرم است. گرافن سختترین و نازکترین مادهای است که بشر تاکنون بهآن دست یافتهاست. این ماده با وجود اینکه ساختار متراکمی دارد، به علت ضخامت بسیار اندکش که برابر با ضخامت یک اتم کربن است، نور را از خود عبور میدهد و از شفافیت 97,3 درصد برخوردار است.
گرافن سختترین و نازکترین مادهای است که بشر تاکنون بهآن دست یافتهاست. این ماده با وجود اینکه ساختار متراکمی دارد، به علت ضخامت بسیار اندکش که برابر با ضخامت یک اتم کربن است، نور را از خود عبور میدهد و از شفافیت 97,3 درصد برخوردار است؛ همچنین آسانی تهیه و رسانا بودن این ماده و قابلیت آن در عبور دادن گرما و جریان الکتریسیته آنرا به گزینهای جدید برای استفاده در پنلهای نوری و کامپیوترها تبدیل کردهاست.شاید به همین دلیل است که از این ماده در ساخت نمایشگرهای لمسی بسیار ظریف و مقاوم استفاده خواهد شد.هم اکنون گرافن درحال نفوذ به کاربرد های الکترونیکی می باشد وممکن است بزودی پایه واساس تجهیزات الکترونیکی را عوض کند.با استفاده از گرافن ،ساخت وسایل برقی کوچک،قابل انعطاف وکم هزینه ،ممکن خواهد بود.
در همین راستا، سامسونگ و آیبی ام از جمله شرکتهایی هستند که قصد دارند این ماده نوظهور را به صورت کاربردی مورد استفاده قرار دهند. جیمز هون، استاد مهندسی مکانیک دانشگاه کلمبیا میگوید: "پژوهشهای ما گرافن را به عنوان مستحکمترین ماده شناخته شده تاکنون ثبت کرده است. گرافن 200 برابر قویتر از فولاد است و برای این که یک مداد بتواند یک ورقه نازک گرافن را سوراخ کند، باید وزن یک فیل را به آن اعمال کرد".
کاربردهای متعدد گرافن حتی از خواصش نیز شگفتانگیزتر است. گرافن حتی یک ماده هم نیست، بلکه طیف بسیار گستردهای از مواد است. از این حیث میتوان آن را با پلاستیک مقایسه کرد. میتوان آن را در هر جایی بهکار برد، از مواد کامپوزیت مثل فیبر کربنی گرفته تا صنایع الکترونیک.
از آنجاکه خواص گرافن هنوز ناشناخته است، هر روز دانشمندان بیشتری به کار بر روی پروژههای آن علاقمند میشوند. اکنون حدود 200 شرکت به پژوهش بر روی گرافن مشغولند و فقط در سال 2010 تقریبا 3000 مقاله در مورد آن منتشر شده است.
فواید آن برای شرکتها و مصرفکنندگان هم کاملا روشن است: ابزارهای سریعتر و ارزانتر که باریکتر و انعطافپذیرترند. به این فکر کنید که گوشی هوشمند خود را لوله کنید و مانند مداد نجاران، پشت گوش بگذارید! اگر گرافن را با کاربردهای امروزی پلاستیک مقایسه کنیم، باید به انتظار روزی باشیم که همه چیز، از پاکت میوه گرفته تا لباسها، دیجیتال شوند. کارتهای ارتباطی آینده، توان پردازشی به اندازه موبایلهای هوشمند امروزی خواهند داشت. گرافن میتواند کاربردهای کاملا جدیدی در ابزارهای الکترونیکی شفاف، انعطافپذیر و بسیار سریعتر از امروز پیدا کند. یک مثال از استفادههای دیگر آن میتواند افزودن پودر گرافن به تایرها برای قویتر کردن آنها باشد.
صفحهی مختصات گرافنی
صفحهی مختصات کارتزین یا دکارتی معروف را میشناسید. این صفحه، شبکهای است که از مربعهایی با طول و عرض واحد تشکیل شده است. در این صفحه دو بردار یکهی i و j هریک به طول یک واحد وجود دارد که توسط آنها میتوان از نقطهی مبدا به هر نقطهی دیگری مثل (nوm) رفت. این کار با تعریف یک بردار به شکل k=mi+njامکان پذیر میگردد.
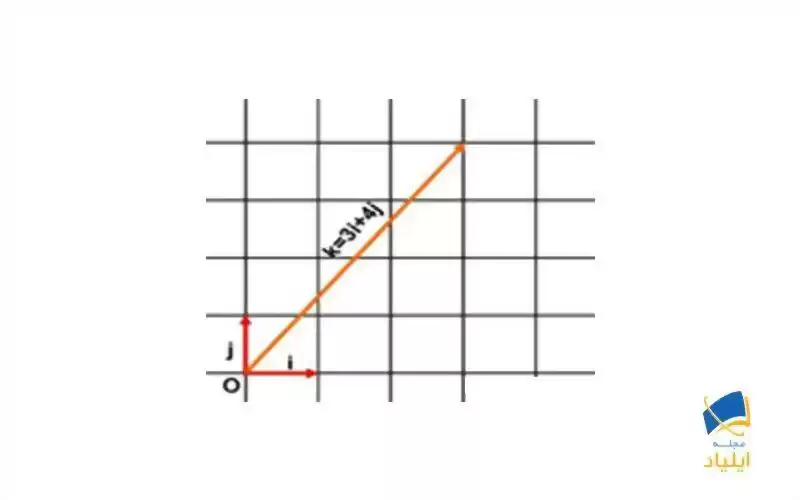
صفحهی مختصات دکارتی؛ بردارهای یکهی iو j هم اندازه و بر یکدیگر عمود هستند
دستگاه مختصات کارتزین، یک دستگاه دو بعدی است که در آن دو بردار یکهی یاد شده، هم اندازه بوده و بر یکدیگر عمود هستند. اما باید توجه داشت که تمام دستگاههای مختصات به این شکل نیستند. بلکه میتوان دستگاه هایی را تعریف کرد که در آن اندازهی بردارهای یکه نابرابر و زاویهی بین آن دو مقدار دیگری باشد مانند صفحهی مختصات گرافنی. صفحهی مختصات گرافنی یک صفحهی دو بعدی متشکل از ششضلعیهای منتظم می باشد. این صفحه یادآور شکل منظم کندوی زنبورهای عسل است.
در این صفحهیِ مختصاتِ دو بعدی، دو بردار یکهی هم اندازهی iو j را به طوری که در تصویر نشان داده شده است، تعریف میکنیم. زاویهی بین این دو بردار برابر با 60° است. برای حرکت روی این صفحه میتوانیم بردار C=mi+nj را تعریف نماییم. این بردار را بردار کایرال مینامیم. به عنوان نمونه ما چند بردار دلخواه را با شروع از یک نقطه، به عنوان مبدا، در تصویر 4 رسم کردهایم.
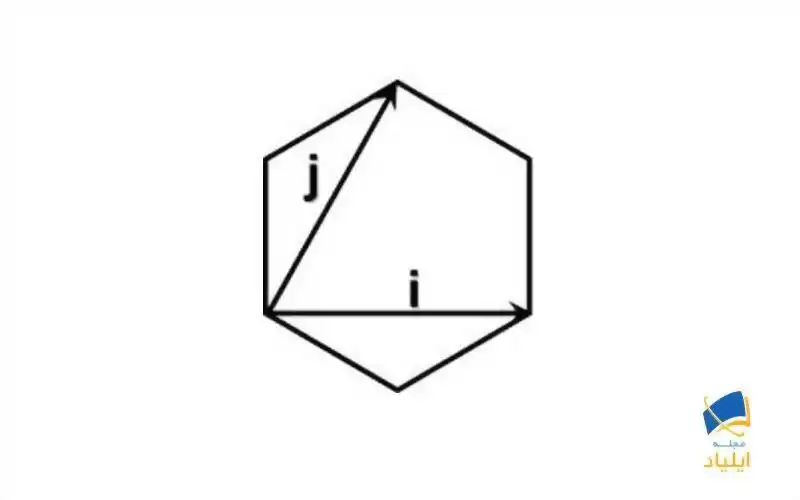

بردارهای یکهی i و j در صفحهی مختصات گرافنی
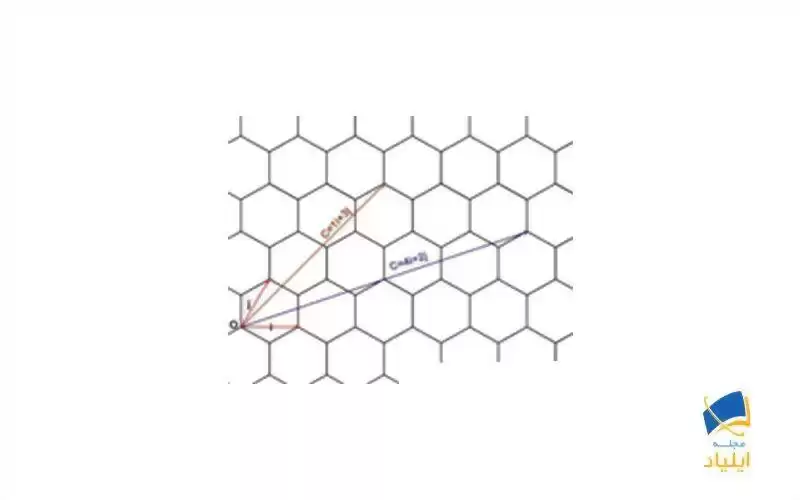
بردارهای کایرال c=4i+2j و c=i+3j در صفحهی مختصات گرافنی
همچنین میتوانیم زاویهی بین بردار کایرال و محور متناظر با بردار یکهی i را به عنوان زاویه کایرال که مشخصهی راستای بردار کایرال است در نظر بگیریم. این زاویه در تصویر 5 نشان داده شده است. همانطور که در آینده خواهیم دید، این زاویه یکی از مشخصههای نانولولههای کربنی میباشد.
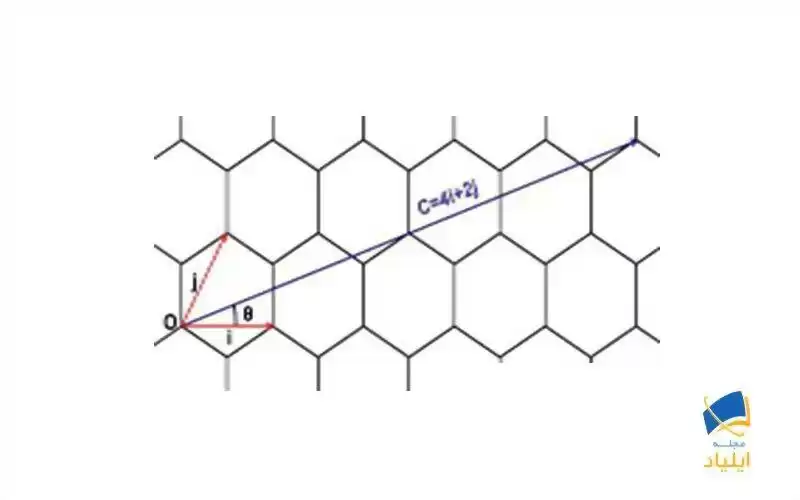
زاویهی کایرال بین بردار c=4i+3j و محور مربوط به بردار یکهی i

